10346. Великое
возрождение (серебро)
Из-за продолжительной засухи
пастбища фермера Джона остались без травы. Однако с приближением сезона дождей пришло время “возделывать растительность”. В сарае
фермера Джона имеется два ведра, в каждом из которых находятся семена разной
травы. Он хочет посадить траву на каждом из своих n пастбищ. Каждое
пастбище должно быть засеяно ровно одним видом травы.
Фермер Джон, занимающийся
молочным животноводством, хочет быть уверенным в том, что он удовлетворит
особые диетические потребности своих m коров. У каждой из его m коров
имеются два любимых пастбища. У некоторых коров имеется диетическое
ограничение: они должны постоянно есть только один вид травы – поэтому фермер
Джон хочет, чтобы на двух любимых полях любой такой коровы был посажен один и
тот же тип травы. У других коров совсем другие диетические ограничения,
требующие от них есть разные виды травы. Что касается этих коров, фермер Джон,
конечно же, хочет, чтобы на двух их любимых полях были разные типы травы.
Помогите фермеру Джону определить
количество различных способов посадки травы на его n пастбищах.
Вход. Первая строка содержит числа n (2 ≤ n ≤ 105) и m (1 ≤ m ≤ 105). Каждая из
следующих m строк содержит символ ‘S’ или ‘D’, за которым следуют два целых числа в диапазоне 1 … n, описывающий пару пастбищ,
являющиеся любимыми для одной из коров фермера Джона. Символ ‘S’ означает, что корове на ее двух
любимых пастбищах нужна трава одного типа. Символ ‘D’ означает, что корове на пастбищах
нужны разные типы трав.
Выход. Выведите количество способов, которыми фермер Джон может посадить траву на n пастбищах. Запишите ответ в двоичном формате.
|
Пример входа
1 |
Пример выхода
1 |
|
3 2 S 1 2 D 3 2 |
10 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
9 10 S 1 2 S 4 5 D 1 5 D 2 4 D 2 5 D 5 3 S 6 7 S 8 9 D 6 9 D 8 7 |
100 |
РЕШЕНИЕ
поиск в глубину
Анализ алгоритма
Построим два графа из n
вершин. Ребра первого графа g1 будут соответствовать пожеланиям коров с символом ‘S’, второго графа g2 – пожеланиям коров с символом ‘D’. Разобьём неориентированный
граф на компоненты связности. Каждая компонента связности должна представлять
собой двудольный граф, где ребра из g1 соединяют вершины из одной компоненты, а ребра из g2 соединяют вершины из разных
компонент. Это свойство компоненты проверим, раскрасив вершины двумя цветами.
Если некоторая компонента не удовлетворяет указанному свойству, то ответ равен
0.
Каждую
компоненту связности можно раскрасить двумя цветами двумя способами (левую долю
цветом 1, правую – цветом 2, или наоборот). Следовательно cnt
компонент можно раскрасить 2cnt способами. Количество
возможных раскрасок равно числу способов, которыми фермер Джон может посадить траву на n пастбищах.
Пример
Граф из
первого теста имеет следующий вид:
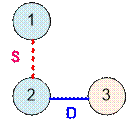
Он
двудольный, его можно покрасить двумя цветами двумя способами.
Граф из
второго теста состоит из двух компонент связности:
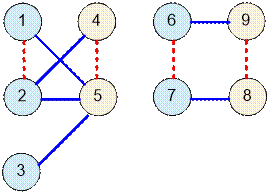
Каждая
компонента связности является двудольной. Граф двумя цветами можно покрасить 4
способами, что в двоичном коде равно 100.
Реализация алгоритма
Объявим графы g1 и g2, а
также массив использованных вершин used.
vector<vector<int>> g1, g2;
vector<int> used;
Функция dfs совершает
поиск в глубину из вершины v. Вершина v
красится цветом color. Функция dfs проверяет, является ли
текущая компонента связности двудольной, причем ребра из g1 должны соединять вершины из
одной компоненты, а ребра из g2 должны
соединять вершины из разных компонент. Если это условие не выполняется,
установим flag = 1.
void dfs(int v, int color)
{
Присваиваем цвет вершине v.
used[v] = color;
Перебираем ребра (v, to) в
графе g1. Вершины v и to должны
иметь одинаковый цвет.
for (int to : g1[v]) // same color
{
Если вершины v и to имеют
разный цвет, текущая компонента не удовлетворяет условию.
if (used[to] == 3 - color) flag = 1;
Если вершина to еще не
покрашена, то продолжаем из нее поиск в глубину. При этом цвет вершины to должен
совпадать с цветом вершины v.
if (used[to] == 0) dfs(to, color);
}
Перебираем ребра (v, to) в
графе g2. Вершины
v и to должны
иметь разный цвет.
for (int to : g2[v]) // different color
Если вершины v и to имеют
одинаковый цвет, текущая компонента не удовлетворяет условию.
if (used[to] == color) flag = 1;
Если вершина to еще не
покрашена, то продолжаем из нее поиск в глубину. При этом цвет вершины to должен
быть отличным от цвета вершины v.
if (used[to] == 0) dfs(to, 3 - color);
}
}
Основная часть программы. Читаем входные данные.
cin >> n >> m;
g1.resize(n
+ 1);
g2.resize(n
+ 1);
Читаем информацию про диетические ограничения коров.
Строим два графа g1 и g2.
for (i = 0; i < m; i++)
{
cin >> ch >> a >> b;
if (ch == 'S') // same
{
g1[a].push_back(b);
g1[b].push_back(a);
}
else // different
{
g2[a].push_back(b);
g2[b].push_back(a);
}
}
Запускаем поиск в глубину на несвязном графе.
Подсчитываем количество компонент связности cnt.
Изначально положим flag = 0, считая что все компоненты
двудольные и удовлетворяют указанному свойству.
used.resize(n
+ 1);
flag = cnt
= 0;
for (i = 1; i <= n; i++)
if (used[i] == 0)
{
Вершину i красим
цветом 1.
dfs(i, 1);
cnt++;
}
Если flag = 1, то
ответ 0.
if (flag == 1)
cout << "0" << endl;
else
{
Выводим ответ 2cnt в
двоичном коде: одна единица и cnt нулей.
cout << "1";
for (i = 0; i < cnt; i++)
cout << "0";
cout << endl;
}